The suggestion has been made several times in this manual that the operator gain information about the elite by using sampling. Such suggestions may have created a common sense image of "tasting a bit of what’s in the kettle" for some and for others may have conjured up frightening statistical visions. Actually, the sampling which the operator can engage in need be neither so simple as to be dangerous, nor so complex as to be frightening. It is the purpose of this Appendix to strike a middle ground, recognizing that in most instances the operator is not prepared to use the more complex statistical tools, but also recognizing that he needs some minimum equipment to use sampling wisely.
By sample is meant any fraction of a total population, or as the statistician says, of a universe. Whenever one examines less than a total population – of persons, books, wheat, iron ore, families – he examines a sample. And the sample, no matter how it is drawn from the total population, will have some of the characteristics of the total population. The hope is that it will have most of the characteristics and that information obtained from it can be "projected" to the population.
At the outset of this discussion, it is important to make clear that the statistical approach to sampling is basically an extension of that of a logical man to the problem inherent in examining a part of anything and then talking about the whole. The logical man recognizes – at least vaguely – the chance factors which limit the usefulness of any sample; the statistician has developed mathematical devices to speak about these chance factors more precisely. None of what is to follow will destroy any previously-used logicalapproaches of the operator. An appreciation of statistical treatment will only rarely demonstrate that previous approaches thought to be logical are in fact fallacious; most of the time, it will only make it possible to be more precise about them.
WHY SAMPLE?
Generally speaking, one examines a sample because (1) he wishes to know something about the total population: (2) it is impossible or impractical to measure the entire population. To emphasize these points, one is not interested in the characteristics of the sample for themselves alone. They invariably are interesting or useful only to the degree that they can be projected to the total population. The impossibility of measuring the total population may be in terms of time or money, possibly even in terms of physical unavailability. Moreover, it may often be that measurement by sampling will be just as accurate as measuring the population.
POPULATION IN A STATISTICAL SENSE
A population or universe is the total collection of units of the same class as those taken in the sample. Defining the given population in a given sampling situation is an arbitrary thing. The sampler can decide that his population will be all of the living human beings in a certain geographic area, or he may limit it to men over thirty-five years of age. It could be all of the books in a certain library, or it could be just those books classified under all numbers referring to political science. If the entire population has been measured, the result is called a census. If qualities and characteristics of the total population have been obtained and have been expressed in numbers, they are called parameters of the population.
While definition of the population under study is arbitrary, it is usually advisable to define it in such a way that it is possible to get at all the individuals in it. Thus when a sampler is interested in a particular population buried or intermingled in a larger population, and there is no ready way to subdivide them, he had best accept the larger group which is available and accessible. In terms of elite study, this might mean sampling from fairly large populations in which the elite might be "intermingled" unless the operator possessed information making it possible to delimit the population because of parameters which were available to him. As a general rule, however, the sampler seeks to make his population or universe as small as possible, to limit the area under study.
WHEN NOT TO SAMPLE
There is a time and place for sampling. It may seem unnecessary to mention it, but a regular warning is this; Don’t sample until you are certain that the information you seek is not available elsewhere. A surprising amount of information is available and it is senseless to go through a sampling study when a census of the information one seeks is tucked away in the recess of some library.
Another warning, which will be expanded upon later, is this: Don’t sample when you can determine in advance that the results of your study cannot possibly give you information of sufficient precision to meet requirements which may be imposed upon you.
A final suggestion: Don’t sample when you are quite certain that the quality or characteristic you seek to measure to the population is very rare. In a sense, this is a restatement of the second warning. To make it specific, if the hypothesis is that .001 per cent of a population possesses a given characteristic, it is almost hopeless to seek to measure this by sampling the total population.
REPRESENTATIVENESS OF A SAMPLE
It was noted above that any sample, no matter how it is taken from the population, will have some of the characteristics of the population. In this sense, it "represents" the population. The degree of representativeness is expressed in terms of measurements of the sample and measurements of the population. If the sample is of males and females from a population equally divided between the sexes, the sample would be perfectly representative of this characteristic if it were also divided 50-50. One can see that a check on the sex-ratio in the population based on taking samples of two, has three possible results – one which is perfectly representative, one which over-represents males and one which over-represents females.
Since the purpose of sampling is to project the measurements of the sample to the total population, the sample hopes to restrict the chances of studying a part of a population which has a low degree of representativeness. In particular, he hopes to get rid of practices on his own part, which will mean that the sample will be non-representative. If one endeavors to determine the sex ratio by a sample of two persons, it would be almost certain that it would over-represent females if one chose the first two persons to come out of the door of a girls’ school. And taking two names from a list of trade union leaders would almost certainly produce two men. Checking at the doors of American homes in the afternoon would probably over-represent women and taking two persons out of a fight audience would over-represent men.
If it could be arranged that every person in this population, made up half of males and half of females, had an equal chance of coming into the sample, there would be a better chance of getting a representative sample (size two) since one out of two times the correct ratio would be obtained. (There are two ways to get a 50-50 split, only one way to get an all-male sample, and only one way to get an all-female sample.)
HOW TO OBTAIN REPRESENTATIVENESS
It is of little value to measure an unrepresentative sample of the population. The results, if projected, will give a false picture. How then to determine in advance that the sample will be representative?
One method involved the use of the parameters of the population. If several measurements are available, it will be possible to construct a sample which will be a fairly exact replica of the population, as far as these parameters are concerned.
It is not certain at all, but the chances are frequently good that such a sample will also be like the general population in the unknown characteristic, provided it is correlated with the known measurements. This sampling method is usually referred to as "quota" sampling. Sometimes small samples, which will serve as a continuing "panel" to be studied on successive occasions, are also chosen by this system.
Another method involved taking individuals from the population complete by chance (in a statistical sense). In this system, care is taken to see that each individual in the population has an equal (or known) chance of being chosen. The sample is then drawn by a method which prevents the researcher from exercising control over the choice of any individual. In working with small populations, it is possible to do this by assigning numbers to every individual and then drawing the desired sample "from a hat" or in a way analogous to that. It is called simple random sampling.
MEANING OF ‘BIAS’
If the sampler takes a chunk of individuals from the population because they happen to be handy, or because they "look" representative, or because they are his friends and don’t mind being questioned, he will have no assurance that his sample will be representative. Most often, his sample will be biased, i.e., the very nature of the drawing of such a sample will mean that if the process were repeated, certain portions of population would be over-represented (or under-represented) consistently. Suppose one took his sample from the crowd passing his office door on a busy street. Some persons would pass by this door so regularly that their chance of coming into the sample would be very high – almost a certainty. Some other persons in the population of the city might never come by the door. If the office were in the financial district, there would be a preponderance of persons connected with banks and brokerage houses. If it were in a warehouse district, the workers and officials of wholesale firms would predominate.
Actually, if it so happened that the "chunk" taken by this method were made up of individuals who varied in the same way as the population on the factors being studied, this sample would not be biased. But this happy event most often does not occur. The "chunk" sample is usually biased in its very nature, and one projects results from measuring it to the population at his own peril.
MEANING OF RANDOM
The term random was introduced in the above section. It has a special statistical meaning, which is not synonymous with everyday usage. One speaks of a person wandering randomly through a field or making a random choice from a box of candy. Yet such behavior is usually not random at all. The position of the box of candy and the position of the person’s hand may reduce the chances of taking a particular piece; subjective values concerning kinds of candy or colors or attitudes about the presence or absence of nuts will enter into the random choice. Almost all human behavior is non-random to a high degree.
If the operator wishes to check himself, let him endeavor to write down twenty-five one-digit numbers in his best attempt at randomness. Then let him write down the figures 0 to 9 on ten pieces of paper and draw twenty-five times from a hat, recording each number. A comparison of the two lists of numbers will demonstrate the inability of man to be random. One person will over-correct, producing a very even distribution of numbers. Another will over- represent a favorite number. Almost all persons, given such instructions, will tend to write down more numbers one digit removed from each other (because of the normal pattern of counting) than can occur by chance. Almost no-one will write down the same number twice in succession, though such an event can occur by chance. Here is another factor which frequently will have an effect: as a person discovers that he has not written down a particular number, it becomes almost certain that he will chose it next.
Suffice it than to say, that if any sampling scheme calls for a random selection ( or selection purely by chance ) the operator must use methods which will prevent human foibles from making it non-random.
GETTING A BAD SAMPLE BY CHANCE
While random methods of selecting samples have been somewhat exalted here, they are not perfect. They are subject to what is known as sampling error. In a statistical sense, this refers to the possibility that a given sample will tend to give a value which is not representative of the population. This can be demonstrated by considering what happens when one samples in an effort to measure a characteristic which varies considerably from one member to another.
Consider this hypothetical study of age of an elite population. Let us say that there were 100 members of the elite with ages ranging from 22 to 78. Say that the 10 youngest range from 22 to 31 (with one in each age bracket), and the ten oldest from 69 to 78. The 80 remaining are from 31 to 69 years old. If one were attempting to get an estimate of the average age of the population by taking a random sample of 10, it would be possible to draw these 10 youngest or 10 oldest. Even though the true mean of this population were 43, it would be possible to get one sample which would indicate the average age was 26.5 years, and another which would indicate 73.5. These are very bad samples – and could be drawn by chance – but they are only two out of more than seventeen trillion possible samples of size 10 which could be drawn from a population of 100. And all the rest of the possible samples will yield estimates of the mean which will be closer to the true value of 43. Further, while there is only one combination which will yield an average as low as 26.5, there are billions of samples which will yield values between 40 and 45.
To bring the probabilities of this example down to manageable size, suppose that ages were so distributed that exactly 50 of the elite were 40 years old and the other 50 were 46 years old. In such a circumstance, there would be only one chance in 1024 that a sample of 10 would contain ALL persons who were 40 years old, while the chance that the sample would contain half 40 and half 46 (and would be exactly representative of the true average age) would be approximately 1 out of 5. Additional probabilities that the average 10 chosen would fall in more or less equal numbers around the mean would add to the probabilities of the result being usefully realistic.
The above examples were set up so that the populations from which the examples were taken were approximately "normal." Normal has both a statistical and a general sense. To take the latter first, normality of distribution is what one sees in nature; people vary from one extreme to another in size, height, income, number of children, with most of them being concentrated about a central value in the vicinity of the midpoint between two extremes. This is true of a tremendous number of measurements, not only of human populations, but of animal populations, inanimate objects, in fact of a considerable percentage of the distributions of measurements that man has taken.
This concentration of cases around a central value means that there are almost always more possible samples which will give values near to the true population mean, than those which are far removed.
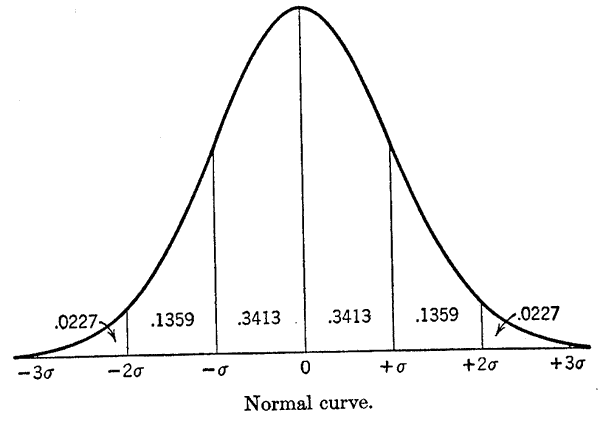
Normality in a statistical sense has a more precise meaning, which indicates that exact proportions of the values of individuals in a distribution will be a certain amount greater or lesser than the central value. This kind of regularity is the basis of much of the statistical treatment of sampling.
To be specific about the normal distribution, it can be stated that 68 per cent of the cases in it will have values which are no more than one "standard deviation" greater than the mean, or no less than one "standard deviation" less than the mean. (The term standard deviation will be taken up in subsequent paragraphs.) Further, 95 per cent of the cases will occur between two values represented by the mean minus two standard deviations and the mean plus two standard deviations.
Departures from normality in a distribution are spoken of by the statistician as "skewness." This refers to a concentration of values either higher or lower than the mid-point of the range between the extremes. If the values are greater the distribution is said to be skewed to the right; if they are smaller, it is skewed to the left.
CENTRAL VALUES
In order to speak more precisely about a population (or a distribution of characteristics of a population) it is necessary to have some meaningful system of combining individual characteristics into a group characteristic. In talking about the normal distribution, we have already introduced several terms which help describe a distribution. One of these is the mid-range, which is the point equi-distant from the extreme values.
A common measurement of central value used universally is the average, or as the statistician calls it, the mean. It is obtained by adding all of the individual values and dividing by the total number of cases. The median is the point which divides the distribution into equal parts as far as numbers of cases or measurements are concerned. The mode is the point in the distribution on which the largest number of cases fall.
If the distribution were perfectly normal all of these measures of central value would coincide. As it departs from normality, these central values tend to move away from each other. Thus a comparison of these several central measurements can tell considerably about the "shape" of the distribution. If the mean, for example, is to the right of the median, one knows that the distribution is skewed to the right, i.e. there are more higher than average values than there are lower than average values, or the number may be balanced but the differences between the high values and the average is greater than that between the low and the average.
Much of the operator’s work may be in determining how a population is divided, i.e. what proportion has a characteristic and what proportion lacks it. This may seem quite different from measuring a variable such as age, yet it can be conveniently thought of as the same kind of variable and the same statistical approach used. The rationale is this: the presence of the characteristic is recorded as a 1, and the absence as 0. There is then a "distribution" (with only two possible values). The mean is obtained by adding up the "1s" and dividing by the total number of cases, which yields a fraction (identical to the percentage). This approach will be useful later when other statistical measures are considered.
MEASUREMENTS OF DISPERSION
As well as measuring the central values of a distribution, it is useful to measure its dispersion. The range and the standard deviation are such measures.
Another would be obtained by dividing the distribution into four equal parts, or quartiles, by frequency of cases. This might show, for example, in the case of ages of the 100 elite, that the first quartile included those from age 22 to 34; the second from 35 to 40; the third from 41 to 52; and the fourth from 53 to 78. Such a division would indicate that the elite were relatively young – half of them being 40 or under. It would also show a considerable dispersion in the oldest quartile, as well as that the distribution is skewed to the right.
To obtain the standard deviation of a distribution, one first computes a statistic known as the variance. It is obtained by squaring the differences between the individual measurements and the mean, adding them together, and dividing by the number of cases. The square root of the variance is the standard deviation.
This measurement tells about the dispersion of the distribution in two useful ways. First, as can be seen from the operations involved in computing it, the standard deviation tends to emphasize cases which are considerably greater or considerably less than the mean. In the hypothetical study of age of an elite population of 100 (as introduced above but with additional ages and frequencies provided) we would obtain a population standard deviation of about 10 years. This standard deviation would be affected much more by the single person 78 years old, who would contribute (35)2 or 1225 to the variance, than by the several persons 44 years old, each of whom would contribute only (1)2 to the variance.

In combination with the mean, the standard deviation also tells us, depending upon the normality of the distribution, approximately how many cases will be within a given distance from the mean. Thus in the hypothetical study of age, the standard deviation of 10, along with the mean of 43 years, would indicate that about 68 per cent of the cases would be between 33 and 53 years, or that 95 per cent of them would be roughly between 24 and 63 years. Actually, since this population is skewed to the right as the foregoing chart shows, there are somewhat more than 5 per cent of the cases outside of these limits.
As well as telling approximately how many cases can be expected to be found within a given distance from the mean, the relationship between the standard deviation and the mean shows whether this is a very widely dispersed population or a concentrated one. It will be found that as a population is made up of individuals which have very nearly the same values as the mean that the standard deviation will approach zero. And it will be found that as a population is made up of individuals with very different values from the mean, the standard deviation will increase.
SAMPLING ERROR
The standard deviation of a population (in contrast to that of a sample) is usually not known; it would not be available unless a census had been taken, and even then, the computation of it would often be a lengthy, tedious task. But mathematicians have demonstrated a relationship between the standard deviation of a population and the deviation of samples, which makes it possible to talk about chance effects upon representativeness of the sample in a more precise fashion.
The relationship grows out of these facts. If one were to draw successive samples from a population, record the means that they provided, and to measure the distribution (or standard deviation) of these averages, he would find that they tended to describe a normal distribution – even if the original population did not.*
Thus, if repeated samples were drawn from a population, very few means will be more than three standard deviations from the true mean. Further, we can say that generally 68 per cent of the sample means will have a value between two points represented (a) by the population mean minus one standard deviation, and (b) by the population mean plus one standard deviation. Going out two standard deviations in both directions will include a little more than 95 per cent of the sample means.
_______________________________
*It can be shown that no matter what the population from which one is sampling, it is impossible for more than 1/9 of the possible sample estimates to differ from the average of all estimates by more than 3 times the standard deviation of the sample estimates." Hansen, Hurwitz, Madow. Sample Survey Methods and Theory. 1953. p.22.
In addition, it has been shown mathematically that the variance of a distribution of sample means (the square of the standard deviation) has a fixed relationship in regard to the population variance. It is this: the variance of a sampling distribution of averages will be equal to the population variance divided by the number of cases in the successive samples.
The quantity obtained by making this computation is called the sampling error of the sample mean. It will always be smaller than the standard deviation of the sample, and will be reduced as the size of the sample is increased.
USE OF SAMPLE VARIANCE AS ESTIMATE OF POPULATION VARIANCE
This mathematical relationship makes it possible to pull ourselves up by our bootstraps. We can now substitute the sample variance as an "estimate" of the unknown population variance and divide it by the size of the sample. Then taking the square root of this number, we obtain the "sampling error." Applying it through the use of the normal curve factors, we can set up limits within which we would expect the population value to be located a certain percentage of the time.
In the example on elite ages, the sampling error would be obtained in the following manner. The sample variance (100) would be divided by the sample size (10), giving a result of 10. In turn, we would then take the square root of 10, which is approximately 3.1. From this we can infer, on the basis of the one sample, that if we drew successive samples, 68 per cent of the time, the means that the successful samples provided would lie between 39.9 and 46.1 years, or that 95 per cent of the time the means would lie between 36.8 and 49.2 years.
This process of substitution may be used if the sample includes at least 30 cases. It would be of no use, for instance, if the sample of ages taken from the population were only 10.
STANDARD ERROR OF A PROPORTION
The relationship between (a) the measurement of a characteristic of a population which varies in the same fashion as age, and (b) a measurement of the presence or absence of a quality which yields a percentage or proportion has already been established in the subsection on Central Values.
| Number in Sample | Standard Error (in %) of a proportion | 95 per cent Confidence limits (in %) |
|---|---|---|
| 50 | 6.9 | 46.5 - 73.5 |
| 100 | 4.9 | 50.4 - 69.6 |
| 200 | 3.5 | 53.1 - 66.9 |
| 500 | 2.2 | 55.7 - 64.3 |
| 1000 | 1.6 | 56.9 - 63.1 |
| 2000 | 1.1 | 57.8 - 62.2 |
As was noted, the percentage can be thought of as the same as a mean. A similar relationship exists between the standard error of a measurement like age and the standard error of a proportion. The main difference, as far as the operator is concerned, is the ease with which the latter may be calculated.
The standard error of a proportion is obtained by multiplying the obtained proportion (usually called "p") by l-minus-the-proportion (called "l-p" or "q"), dividing the result by the number of cases in the sample (usually called "n"), and taking the square root of the final result. In formula form this looks like this: √(p x q) .The result is the
√ n
standard error of the proportion, and like the standard error of a sample mean, is used to indicate the percentage of all possible samples which can be expected to yield proportions (means) within certain limits.
For most of the operator’s purposes, it will be sufficient to use the 95 per cent confidence level, which sets up limits based on the obtained proportion, plus approximately two times the standard error (actually 1.96) minus two times the standard error. As can be seen from the formula, this standard error of a proportion will very in accordance with the obtained proportions, getting smaller as they become more extreme; it will also vary with sample size, getting smaller as the sample size increases. The confidence limits will accordingly shrink (or expand) at the same time.
An idea of how sample size will affect the standard error of a proportion is provided in the following table, based in each instance on an obtained value of 60 per cent:
These values will always be obtained when the sample is of the size indicated, when the percentage is 60 per cent, and when the 95 per cent confidence level is used. Similar tables could be worked out for every percentage.
One caution on the use of the standard error of a proportion should be made. If the division of the sample is very extreme (beyond a 90%-10% split) and there are less than five cases in the smaller percentage, this formula should not be used.
Another caution relates to the use of breakdowns. Thus, a study might indicate that an elite population is divided 60 to 40 in favor of the U.S., with confidence limited based on a sample of 200. Breakdowns of the figures might show that the sample contained 50 members of Party A, of whom 60 per cent were favorable, 20 of Party B, with 50 percent favorable; 20 of Party C, with 75 per cent favorable, and 10 of Party D, with 50 per cent. The confidence limits of each of these percentages must be based on the number of cases in each of the sub-samples, rather than on the total sample. Obviously, as far as the universe of Party A members is concerned, one has only a sample of 50 upon which to base his estimate (and similarly for each of the subsequent cases).
THE FINITE MULTIPLIER
In most sampling to obtain proportions, the population is very large in relationship to the sample. However, if the population is somewhat smaller and the sample represents a fairly large part of it, it becomes useful to consider a factor known as the finite multiplier. This factor works to reduce the standard error and, as a result, to give more confidence in the results. Since the operator will quite often be sampling from rather small populations, the possibility of his using this factor is increased.
The finite multiplier is represented by that portion of the population which is not drawn into the sample. Thus, if the sample represented 1/10th of the population, the finite multiplier would be 9/10th s. The figure obtained by completing the p x q is multiplied by the finite n multiplier, and the square root is taken of the resulting figure. Since the multiplier will always be less than l, the resulting standard error will always be smaller. The larger the percentage of the population taken, the more the standard error is reduced, until the entire population has been taken, in which case it is reduced to O.
There is obviously little to be gained by using the multiplier when 1/100th or less of the population has been taken in the sample, since the multiplier will be .99 or larger and the change in the standard error will be almost imperceptible.
EXAMPLES OF USE OF STANDARD ERROR OF PROPORTION
Let us now apply the information of the last two subsections on some specific examples. Suppose the operator had a card file of 1000 members of the elite which he had gathered from various sources, containing considerable information which had not been analyzed. Suppose he is interested in a quick study of several characteristics of the elite, such as membership or lack of it in a religious group; attendance or lack of it at a university. Let him draw a sample of 50 by random methods, and suppose that his results show that 40 per cent of his sample are members of religious sects and that 55 per cent attended university.
The formula for the standard error of a proportion would be applied in this fashion. For the obtained value of 40 per cent, he would multiply .4 x .6, getting .24. This would be divided by 50, giving .0048. Since he took 5/100ths of the population, the finite multiplier would be 95/100ths. This would give a value of .00456. The square root of this is approximately .68 (or 6.8 %). The same kind of computation of the 55 per cent value would give a standard error of 6.9 per cent. Calculating the confidence limits at the 95 per cent confidence levels would give limits of from 26.7 to 53.3 per cent for the religious affiliation figure and from 41.5 to 68.5 for attendance in college.
If the operator had taken 200 of his 1000 population, much narrower confidence limits would be obtained. Gaining both from the increase in sample size and the decrease in the finite multiplier, the two standard errors would be very considerably reduced, down to 3.1 for the religious affiliation figure, and to 3.3% for the college education result. This would result in confidence limits of from 33.9 to 66.1 for the religious affiliation and of 48.5 to 61.5 for the college attendance.
CHOOSING SIZE OF SAMPLE
Since sample size has such large effects on the confidence with which one may use the results, it becomes a key question in any sampling operation. What size sample is enough? The exact answer, in any given situation, is something like the old riddle about the length of a piece of string – it has to be long enough to go around whatever one wants to tie up.
Thus, it is up to the operator to decide in advance how precise a result he wishes. He can always determine the broadest part of the possible confidence belts by assuming an obtained result of 50 per cent, and by calculating the confidence limits based on the size of the sample and its relationship to the total size of the population. If this result, which will be his worst or largest confidence limits, seems too imprecise to be of value for his purpose, the operator had better increase the size of the sample until he reaches limits more acceptable for his purposes.
Some notion of the gain in precision which comes from increasing sample size is shown in the example three paragraphs before. By quadrupling the sample, the size of the standard error was cut a little more than half (the extra gain coming because of the decrease in the size of the finite multiplier). This relationship will hold generally; to reduce the sampling error by an amount equal to any factor, it is necessary to increase the sample size by the square of the factor (less whatever benefits accrue from taking a larger percentage of the population).
REQUIREMENT FOR SIMPLE RANDOM SAMPLING
All of the statistics of sampling are based upon the premise that the sample is drawn in a random fashion. Several factors which relate to this have already been taken up, but the requirements for the drawing of such a sample will be spelled out in detail here.
1. The total population must be available.
2. Numbers must be given to each individual in the population.
3. The sample must be taken from this "list" of numbers in a completely random fashion.
4. There must be no substitution of individuals drawn in the sample.
AREA SAMPLING
A modification of the simple random sampling method which can sometimes be used is what is known as "area sampling." In such a case it is impossible (or difficult) to enumerate the entire population, but it is possible to enumerate some subsidiary list (usually much smaller than the total population) to which the individual units can be "attached."
The system is most often applied in drawing a random sample of households in a large city, or from a nation as a whole. In the U.S. case, generally a list of counties is made, numbers are attached, and a sample of counties is drawn. Then the chosen counties are split up into geographical sub-areas, and a sample of these are taken. By successive steps, the sampler moves down to smaller geographical units, finally choosing dwelling units in blocks, and individuals within the dwelling units, each step being performed in a random manner. Then interviewers visit the specific individuals selected by this process, getting their opinions, attitudes and behavior.
Such a device requires excellent maps of the area to be studied. In addition, if there are very considerable differences in the population sizes of the various sub-sections it may be advisable to do what it called "sampling in proportion to size." This method simply calls for allowing counties, or other chosen units, additional chances of being selected in accordance with their population. Thus one would give a county with a population of 10,000/10 opportunities to come into the sample (by assigning 10 numbers to it instead of 1) and would give a county with only 1000 population only 1 chance to come into the sample.
Generally speaking, the operator will probably have little opportunity or need to use the area sampling method in this sense. However, sampling systems analogous to it may be used in keeping with the kinds of problem that he will face.
For example, if the operator wanted to sample a voluminous edition of a book like Who’s Who, he could use a modification of this system. He could divide to total volume into pages (after a check to determine that the number of biographies per page was roughly the same), and then draw one name from each page by some standardized system (such as taking the 5th name from the top of the page in the left hand column, or some other number drawn at random). If the book were very large, he might even take every other page. If he had a table of random numbers, he could draw a set of numbers which would govern which page he took.
QUOTA SAMPLING
A methodology long used in the United States, particularly by public opinion pollers is what is called "quota sampling." In this methodology, a considerable number of characteristics of the population are known as the result of various censuses. The sampler, then, endeavors to build up a sample which has the same characteristics as the universe. Taking such measures as sex ratio, age, economy status, education, political affiliation and other divisions of the population, which are known, he selects individuals who fit the "quota" which he sets up.
Thus, if the operator had available several parameters of the total elite population, such as age, sex, political affiliation, membership in church organization, job or skill classification, he might put together a sample which would have the same proportions, with some hope that it would be representative of the universe in the characteristic he wished to measure as well as the known parameters.
Two problems arise with this methodology. First, it is necessary that the unknown characteristics vary along with (or be correlated with) the known characteristics. Thus, if he were endeavoring to measure favorableness to U.S. messages in an elite population, and it happened that this quality did not vary with age, sex, political affiliation, and church membership, he might obtain a very unrepresentative sample, despite careful polling of quotas along the proportion of these traits. The chances, of course, are that if a sample is controlled in several basic, characteristics, it will also be controlled in the characteristic under study. Secondly, this method makes it inadvisable to apply the statistical checks which have been suggested above. This arises because of the nature of the selection of individuals to be in the sample. It is almost always NOT random in a statistical sense. As a result, the formulas developed specifically for the testing the confidence limits of random samples cannot be applied. This represents the position of statisticians. In actual practice many persons using quota sampling DO apply statistical tests. The assumption is that they will be indicative of the precision of the results of the quota sampling, even though there is no statistical rationale for their use.
PANEL SAMPLING
Choosing a small sample in a purposive way to make a panel which would be a cross section of the population is actually a special case of quota sampling. As such, it is also impossible to determine sampling error by statistical methods which have been described – or by any other method, for that matter.
A characteristic of the panel is that it is used over and over again. Care must be taken in this process to determined whether the experience of being questioned is influencing the panel in such a way as to make it less representative.
Despite these difficulties, the small panel can often be very illuminating. The information the operator gains from the panel may provide hunches as to the characteristics of the population from which it is drawn. And the combination of panel information with other material available from other sources may make it possible to speak about the population with considerable accuracy.
SIGNS AND SUGGESTIONS
While sampling statistics give an impression of great precision, even the best of methods is far from precise. However, a knowledge of how basic chance factors affect the characteristics of samples is of value to the operator, even if he never calculates a confidence limit, nor figures out a standard deviation. For awareness of the chance factors will suggest to him that he had better go slow at some times, because his result may be primarily the result of chance. The nature of bias in a sampling methodology and the alertness of it, will also suggest greater incredulity when he looks at "hard figures" based on sampling methodology which is inherently faulty.
It is suggested here that several conditions should be noticed by the operator who is doing his own sampling, or who is utilizing material worked up by others. Among these are:
1.Always check a measurement of a central value (average or proportion) against the size of sample and the size of the population.
2. If a measurement of dispersion is available, the larger it is the less confidence one should put in the measurement of central value.
3. If the interest of the operator is in the variation of the population rather than its central value, somewhat smaller sample sizes are acceptable.
4. In evaluating information obtained from large scale sampling, one will find that a properly drawn random sample of 3,000 or more – no matter what the size of the population – usually has high enough precision to make its results quite dependable.
5. Be skeptical of breakdowns from samples which may be adequate in size on major points, but which may have very small numbers of cases on which to base the breakdowns. Thus in the preceding case (4), though the 3000 may be an excellent sample, a comparison of two small pieces of it (say of 20 and 35 cases) will have a much greater probable error than the sample as a whole.
6. Be particularly skeptical of breakdowns of quota samples. Often they are controlled on a limited number of factors. Total divisions of the populations may be based upon representative samples, but breakdowns may be samples which – in effect – have not been controlled.
7. If a sample is identified as a random or probability type, check on the percentage of individuals chosen to be in the sample who were actually measured. Sometimes 25 per cent or more of the chosen sample cannot be reached. This affects adversely the confidence with which one may use the results.
8. Always look for a discussion of the sampling methodology in any report based on taking a part of a population. Generally, if a high quality job has been done, the system used will be described in considerable detail.
Finally, the operator need not let the weight of statistical arguments overwhelm him. He will almost always be in a position where some information is better that no information. If he gains information from a non-random sample it is not rendered useless if it cannot be checked by the methods given here. Such information, combined with other material may provide much insight into the composition of the elite or on the problem of locating its members. The cautions given here should be thought of as relative, not absolute. And when precise sampling techniques can be used to help with the job, they should be used. If the complications in using them are too great, they can be considered uneconomic methods and put aside for a more suitable task. They should never be used just for the sake of using scientific techniques.